SATT(Self-Adjusting Top Tree)学习笔记

前言

1. SATT ，即 Self-Adjusting Top Tree，是 2005 年 Tarjan 和 Werneck 在他们的论文《Self-Adjusting Top Trees》中提出的一种基于 Top Tree 理论的维护完全动态森林的数据结构。

2. 前置知识：Splay 。

3. 笔者第一次写博客，试图将 SATT 讲的通俗易懂，如果发现哪里讲错了也欢迎指出。

目录

$\mathtt{\text{1.问题引入 }}$

$\mathtt{\text{2.树收缩}}$

$\mathtt{\text{2.1 Compress \& Rake }}$

$\mathtt{\text{2.2 簇}}$

$\mathtt{\text{2.3 Top Tree }}$

$\mathtt{\text{3. Self-Adjusting Top Tree }}$

$\mathtt{\text{3.1 原理 }}$

$\mathtt{\text{3.2 结构}}$

$\mathtt{\text{4.代码实现}}$

$\mathtt{\text{4.1 Push 类函数}}$

$\mathtt{\text{4.2 Splay 类函数}}$

$\mathtt{\text{4.3 Access 类函数}}$

$\mathtt{\text{4.4 Link \& Cut}}$

$\mathtt{\text{4.5 完整代码（Luogu P3690 【模板】动态树）}}$

$\mathtt{\text{5.时间复杂度证明}}$

$\mathtt{\text{5.1 势能分析}}$

$\mathtt{\text{5.1-1 势能分析引入}}$

$\mathtt{\text{5.1-2 Splay 复杂度证明}}$

$\mathtt{\text{5.2 SATT 复杂度证明}}$

$\mathtt{\text{6.例题}}$

$\mathtt{\text{7.参考资料 }}$

1.问题引入

维护一个森林，支持如下操作：

• 删除，添加一条边，保证操作前后仍是一个森林。

• 整体修改某棵树上的某条简单路径（表现为将这条路径上的每个点都打上某个标记）。

• 整体修改以某个点为根的子树。

• 整体询问某棵树上的某条简单路径（如询问点的权值和）。

• 整体询问以某个点为根的子树。

2.树收缩

在本章中对 簇，Top Tree 等概念的表述以《Self-Adjusting Top Trees》中的 表述为准。

2.1 Compress & Rake

对于任意一棵树，我们都可以运用树收缩理论来将它收缩为一条边。

具体地，树收缩有两个基本操作：Compress 和 Rake，Compress 操作指定一个度为二的点 $x$，与这个点相邻的那两个点记为 $y$，$z$，我们连一条新边 $yz$；将点 $x$ ，边 $xz$ ，边 $xy$ 的信息放到 $yz$ 中储存，并删去它们。

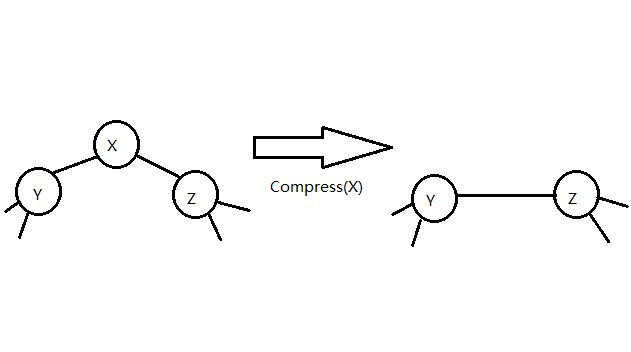
如图 1-1 ,为 Compress 操作。

Rake 操作指定一个度为一的点 $x$ ，这个点的邻点 $y$ 的度数需大于一，设点 $y$ 有一个邻点 $z(x\ne z)$，我们将点 $x$ ，边 $xy$ 的信息放入 边 $yz$ 中储存，并删去它们。

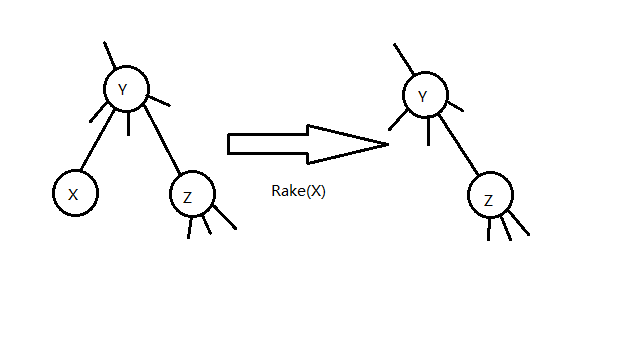
如图 1-2 ,为 Rake 操作。

不难证明，任何一棵树都可以只用 compress 操作 和 rake 操作来将它收缩为一条边。

如图 1-3 ,为 一棵树通过一系列 Compress 、Rake 操作收缩为一条边。

2.2 簇

为了表达方便，我们记在进行任何操作之前的原树为 $T$ 。在对 $T$ 进行某些树收缩操作（可以不做任何操作）之后的树记为 $T_x$。

我们研究 某个 $T_x$ 中某一条边所包含的信息情况。

这条边除了带有它本身的信息（当然，如果这条边在 $T$ 中不存在，这条边就没有“本身的”信息）之外，还可能包含其它通过 compress，rake 操作合并到它上面的点，边的信息。我们不妨先从图1-3中的树收缩过程中选取一条边，看看它所包含的信息在 $T$ 中代表哪些点，边。

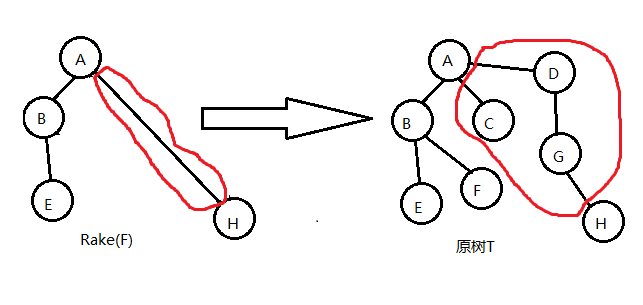
如图 1-4 ，选取的边和对应的图已用红线圈出。

可以看出，这条边所包含的信息在 $T$ 中代表的点，边是连通的（这些点，边组成了一个连通子图）。我们可以推及，对于任一 $T_x$ 中的任一条边储存的信息在 $T$ 中总体现为一个连通子图。我们将这样的连通子图称为簇（cluster）。

然而，簇是不完整的，它包含的某些边的端点不被它自己包含。于是我们将这些端点称作簇的端点（endpoint），将它包含的那些连通子图的点称作内点 （internal node），连通子图的边称作内边。

对于任意一个簇，都有以下性质：

1. 簇只维护内点和内边的信息。

2. 簇有两个端点。这两个端点即为 $T_x$ 中代表那个簇的边相连的那两个点。两个端点之间的路径我们称之为簇路径（cluster path） ；记两个端点分别为 $x$，$y$ ，我们用 $C(x,y)$ 来表示这个簇（在不同的 $T_x$ 中可能会有多个这样的簇）。

3. 内点仅与端点或内点相连，端点可能与非簇点相连。

特别地，对于 不做任何操作的 $T_x$（即为 $T$ ） 中的每条边，其对应的簇只包含代表它的边，这种簇我们称之为 “基簇”（base cluster） 。对于由 $T$ 收缩到只有一条边的最终的 $T_x$，$T_x$中的那条边代表的簇包含除了两个端点之外的整棵 $T$ 的信息，这个簇我们称之为 根簇（root cluster）。

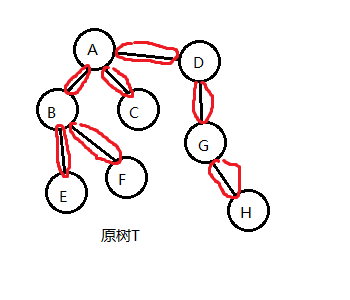
如图 1-4，上文提到的基簇已用红线圈出。

从簇的视角来看Compress，Rake 操作，我们发现这两个操作会将两个簇“合二为一”，剩下一个新簇，所以树收缩的过程也是所有的基簇合并为一个簇的过程。

所以我们也可以得到图1-5，它是与图1-3对应，对一系列树收缩操作的另一表示。

如图 1-5 ，树收缩过程的另一种表述。

2.3 Top Tree

我们现在想表示某一棵树进行树收缩的全过程。

根据上文，可以用图 或图 里的方法来表示这一过程，但这样十分麻烦，如果树收缩进行了 $n$ 步，我们就要用 $n$ 棵树来表示整个树收缩。

考虑一个对某棵树进行某一树收缩的更简便表示，我们引入 Top Tree。

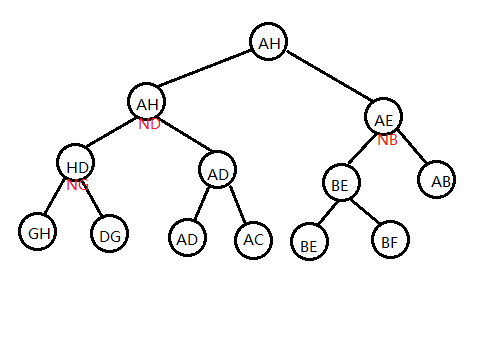
如图1-6，为以图 1-3 的收缩方法和原树为基础的一棵 Top Tree。

Top Tree 有以下性质;

1. 一棵 Top Tree 对应一棵原树和一种树收缩的方法，Top Tree 的每个节点都表示在某个 $T_x$ 中的某一条边，也就是树收缩过程中形成的某一个簇。图中的形如 $N_x$ 的点表示 $compress(x)$ （意义见 2-1）这一操作形成的簇。

2. Top Tree 中的一个节点有两个儿子（都分别代表一个簇），这个节点代表的簇是这两个簇通过 compress 或 rake 操作合并得到的新簇。

3. Top Tree 的叶子节点是基簇，其根节点是根簇。因此我们按一棵 Top Tree 的拓扑序分层，它的每一层就代表了一棵 $T_x$。

3.Self-Adjusting Top Tree

3.1 原理

先要说明一下，这里的 Self-Adjusting Top Tree 与 Tarjan 的原初版本有所不同：没有用到 unit tree 理论，导致最终整棵 SATT 的形态，操作方面有些差异。此外，这篇文章直接将 SATT “三度化”了，并不考虑维护树的一些更精细的结构。

Top Tree 对树收缩过程的极大简化 使我们看到通过维护树收缩过程来维护树上信息的可能性，SATT即是通过这一原理来维护树上信息的。

注意到树收缩的过程也是树上信息不断加入的过程，我们执行一次 $compress(x)$，$x$ 点的信息从此刻起就开始在簇中出现，影响着我们的统计结果。

假如我们现在用 top tree 来维护某棵树 $T$，树上的每个点，边都有权值，我们要维护的是 $T$ 的权值和。(不考虑统计不到端点的问题）

现在我们在维护时要对 $T$ 中某个点 $x$ 的权值进行修改，很明显，我们就需要更改 top tree 中所有簇信息包含 $x$ 的节点信息，这样做显然单次时间复杂度是 $O(n)$ 级别的。

然而，如果我们选的点它在 top tree 中簇信息包含 $x$ 的节点个数很少，也就是说使它的信息尽可能晚地加入簇中，我们单次时间复杂度就会有一个很大的提升。

如图 2-1 ,为上文内容的图片说明。

SATT 就是通过修改 某个点/某条路径 在树收缩过程中信息被加入簇中的先后顺序来维护树上信息的。

3.2 实际结构

我们先将一棵原树 $T$ 分层定根，然后我们考虑对某种树收缩顺序的 top tree 的 根簇，它有两个端点，我们令这其中一个端点就是原树的根，另一个端点任选。

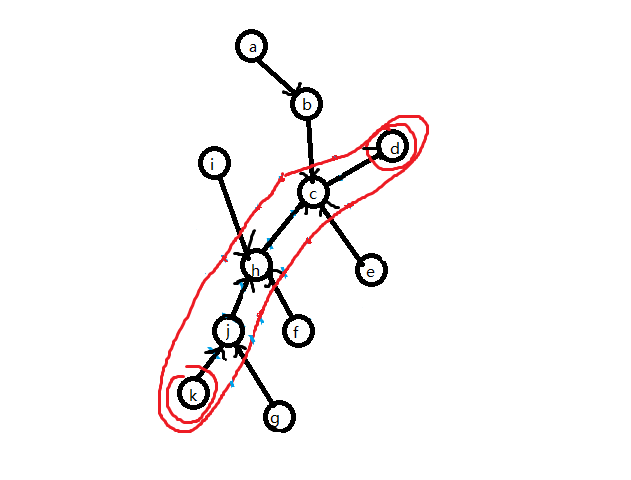
如图 2-2，给根簇选出一组端点，这里标注簇时将端点也圈进去了。

由树收缩的基本操作（2-1）可知，簇路径上的点，边 $(j,h,c,jh,hc)$ 的信息最后是通过 compress 操作才加入 $C(k,g)$ 的，而的非簇路径点 $(a,b,i,f,g,e,ig,\cdots )$ 是通过 rake 操作才加入 $C(k,g)$ 的。

我们将簇路径单独拿出来，这是一条形态特殊（为链）的树，我们为这棵树建出一棵改动后的 top tree（其代表的树收缩顺序任意）。

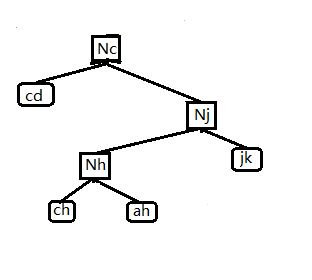
如图2-3，上述的 top tree 。

我们将这一结构称之为 compress tree，因为在这棵 top tree 中任一个点的两个儿子之间是通过 compress 操作来合并成它们的父亲。

compress tree 里的节点称为 compress node。只考虑当前这条簇路径，一个 非叶子的 compress node（必是 $compress(x)$ ） 就代表一次 compress 过程，表示将左儿子和右儿子信息合并起来，再将这个 $compress(x)$ 本身存储的点 $x$ 信息加入。这棵 compress tree 就维护了 $C(k,g)$ 簇路径的信息。

另外，在 compress tree 中，我们实际上还对使用的 top tree 做了一些限制，因为注意到 compress tree 维护的是一个 $T$ 中深度两两不同的链，所以我们规定在 compress tree 中元簇的中序遍历顺序对应的 $T$ 中边的深度是一致的，且中序遍历越小深度越浅。同样，对于每个点 $x$ 对应的 $compress(x)$ 的关系 也是如此。

现在来维护那些非簇路径的信息，我们假设这些 非簇路径上的点 ，边已经形成了一个个极大簇，而这些极大簇是由这些用蓝线圈出的更小簇 rake 形成的，对由一些更小簇合并形成一个极大簇的过程，我们用一个三叉树来表示，类似的，我们称这一结构为 rake tree，对应地 rake tree 里的点就是 rake node。rake node 里面的点都代表一个簇，是由左儿子和右儿子 rake 到其 中儿子代表的更小簇上形成的（不考虑 rake 操作加入 $T$ 中某个点信息的问题）。具体可见下图，可知 rake tree 中的每个点都代表了 $T$ 中具有相同端点的更小簇。

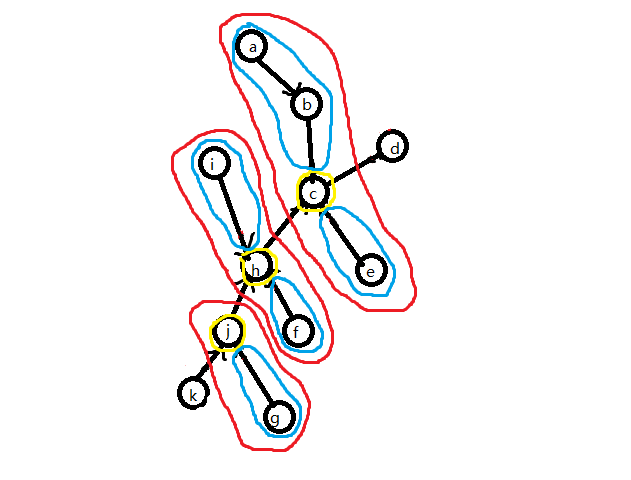
如图2-3，蓝线圈出的是一个个极大簇，黄线圈出的是一个个更小簇。

对于那些更小簇，我们对它们进行相同处理，给它们选择簇路径、建出 compress tree $\cdots$ 如此递归下去，就建出了许多表示树收缩过程的 compress tree，rake tree。

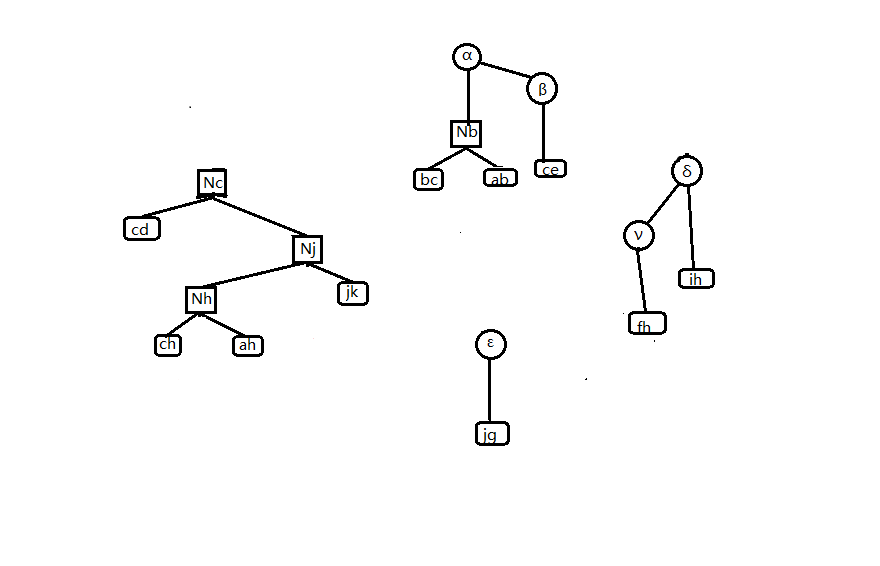
如图2-4，为原树的 rake-compress tree（因为rake node 连着一棵 compress tree，所以表现为一棵 rake tree 连着许多 compress tree 的形态）和代表根簇路径的 compress tree。

考虑将这些树以某种方式拼接在一起，使它们形成一个有序的整体。记一个 rake tree 代表的最小簇的集合的公共端点是 点 $x$。我们给这些 rake node 的中儿子（一个 compress tree 集合）都加入非 $x$ 的另一端点，但仍保持其中序遍历和 top tree 的基本性质。

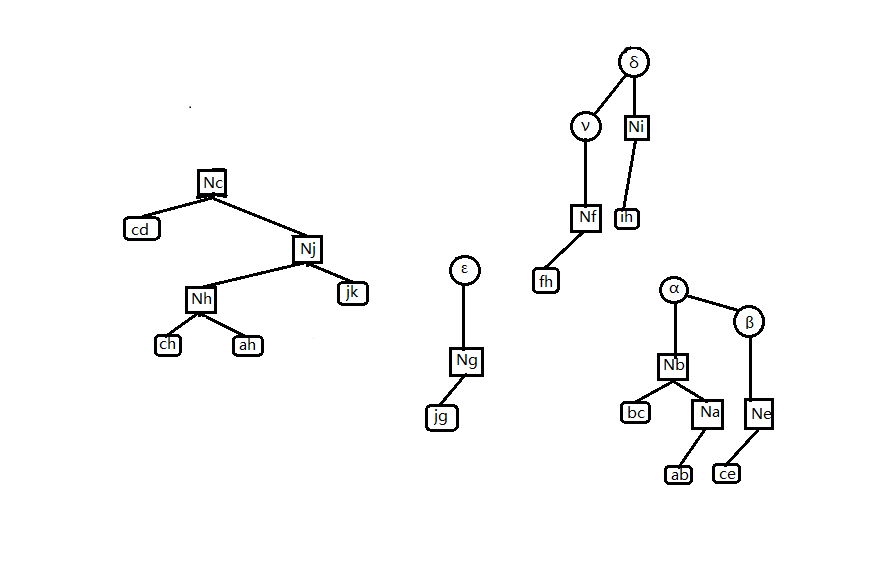
如图 2-5，对图 2-4 进行了上述修改。

这一步相当于是让 rake 操作加入某个 $T$ 中点的操作直接发生在 compress tree 中，这不仅是我们能 正确维护 rake node 的信息（只需将三个儿子信息合并即可），还使我们 compress tree 的结构更“完整”。下一步，我们将 compress tree 改为三叉树，若某个 rake tree 的公共端点是 点 $x$ 我们就将 rake tree 挂在 $compress(x)$ 的中儿子处。

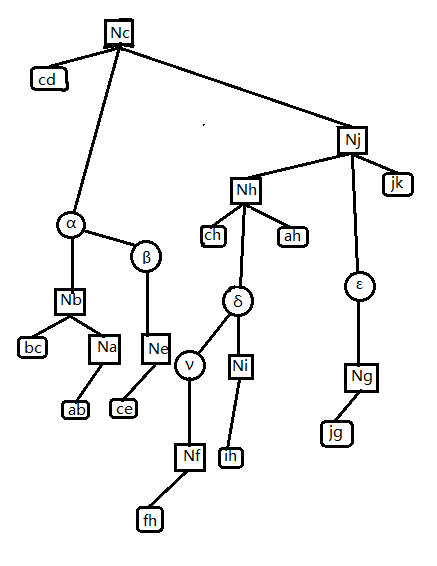
如图2-6，对图2-5进行了上述修改。

此时经过三叉化的 $compress(x)$ 点，它的意义就变成先将其中儿子 rake 到簇路径上，再统计左右儿子 和点 $x$ 的信息。

最后，我们再处理一下根簇路径的那棵 compress tree：与其它所有 compress tree 一致的，按中序遍历加入它的两个端点，使得 它的根储存整棵 $T$ 的信息。

于是我们就得到了一棵 Self-Adjusting Top Tree。

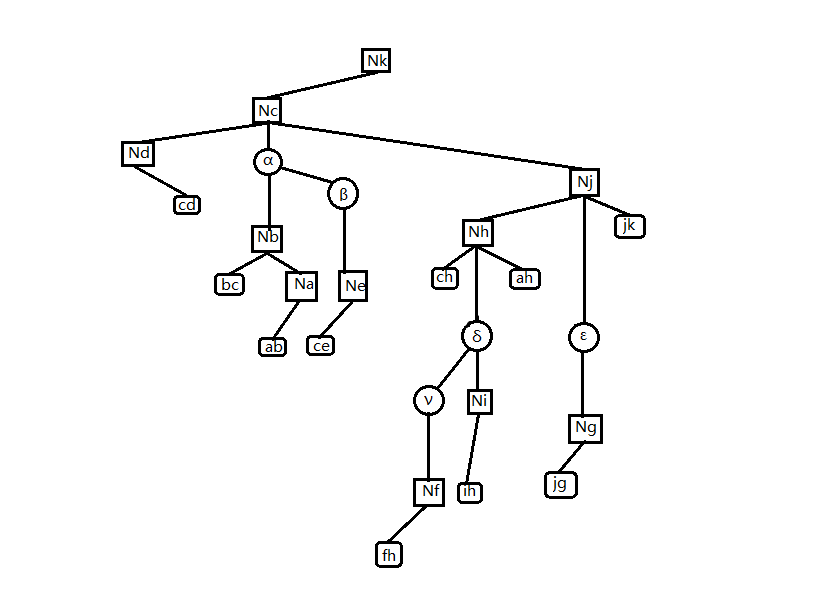
如图2-7，为一棵 Self-Adjusting Top Tree 。

总结一下，SATT 有以下性质：

1. SATT 由 compress tree 和 rake tree 组成，compress tree 是一棵特殊的 top tree；rake tree 是一个三叉树，它们都对应一棵树进行树收缩的过程。

2. compress node 里的点最多有三个儿子，非叶 compress node 可以任意旋转（保持 compress node 中儿子不变）。

3. rake tree 里的点一定有一个中儿子，rake node 可以任意旋转（保持 rake node 中儿子不变）。

4. SATT 的拓扑序反映了原树 $T$ 的树收缩顺序。

我们在 3-1 部分提到的“修改 某个点/某条路径 在树收缩过程中信息被加入簇中的先后顺序”SATT是否能实现呢，答案是肯定的。

在SATT中，有一个 access 的操作，它的作用是使某点 $x$ 在 $T$ 中成为根簇的非根端点，同时在 SATT 中使 $compress(x)$ 成为 SATT 的根。

我们可以通过 access 操作以均摊 $O(logn)$ 的复杂度使 SATT 中代表 $compress(x)$ 的点旋到整棵 SATT 的树根，根据 SATT 的第四个性质，我们改变了$compress(x)$的操作顺序，使得它最晚执行，$x$ 点的信息也就被最晚加入；这样当我们要修改 $x$ 点的信息时，就只需要更新 $compress(x)$ 。

4.代码实现

4.1 Push类函数

Pushup

在考虑对 SATT 的某个节点维护信息时，首先分这个点在 compress tree 还是在 rake tree 进行讨论，原因可见上文，不再赘述，下面以维护某个点的子树大小为例

// ls(x) x的左儿子
// rs(x) x的右儿子
// ms(x) x的中儿子
// type==0 是 compress node
// type==1 是 rake node
void pushup(int x,int type){
    if(type==0)size[x]=size[rs(x)]+size[ms(x)]+1;
    else size[x]=size[rs(x)]+size[ms(x)]+size[ls(x)];
    return;
}

查询点$x$的子树大小，就将其 access 到 SATT 根，答案是其中儿子的 size $+1$ ；因为根据上文，在 access 之后，其中儿子才是它的真子树。

Pushdown

我们如果要对原树中的某个子树做整体修改，一个很自然的想法是：将这个节点直接 access 到 SATT 根节点，给它的中儿子打上一个标记即可。同理，查询子树就直接 access 后查询中儿子。

我们如果要对原树中的某条路径做整体修改，我们就 $expose$ 路径的两个端点，其中 $expose(x,y)$ 是使 点 $x$ 成为了 $T$ 的根节点，使点 $y$ 成为了根簇的另一个端点。对应在 SATT 上，此时根簇 的 compress tree 就是 $x$ 到 $y$ 的路径。于是直接给根簇的 compress tree 打上一个标记即可。同理查询链 $expose$ 后查询根节点即可。

于是我们就知道问题引入的问题怎么做了。。

void pushdown(int x,int type){
    if(type==0){
        //deal with chain
        chain[ls(x)]+=chain[x];
        chain[rs(x)]+=chain[x];
        val[ls(x)]+=chain[x];
        val[rs(x)]+=chain[x];
        //deal with subtree
        subtree[ls(x)]+=subtree[x];
        subtree[rs(x)]+=subtree[x];
        subtree[ms(x)]+=subtree[x];
        val[ls(x)]+=subtree[x];
        val[rs(x)]+=subtree[x];
        val[ms(x)]+=subtree[x];                
        subtree[x]=0;    
    }
    else{
        subtree[ls(x)]+=subtree[x];
        subtree[rs(x)]+=subtree[x];
        subtree[ms(x)]+=subtree[x];
        val[ls(x)]+=subtree[x];
        val[rs(x)]+=subtree[x];
        val[ms(x)]+=subtree[x];                
        subtree[x]=0;            
    }
    return;
}
//下传标记
void pushall(int x,int type){
    if(!isroot(x))pushall(father[x],type);
    pushdown(x,type);
    return;
}

4.2 Splay 类函数

我们知道 SATT 中的 rake tree 和 compress tree 都是可以旋转的，也就是说它们可以用 Splay 来维护。因此我们可以写出以下代码：

// ls 一个SATT节点的左儿子
// rs 一个SATT节点的右儿子
// ms 一个SATT节点的中儿子
// type==1 在rake tree中
// type==0 在compress tree中
bool isroot(int x){return rs(father[x])!=x&&ls(father[x])!=x;}//是一个节点的中儿子或无父亲
bool direction(int x){return rs(father[x])==x;} 
void rotate(int x,int type){
    int y=father[x],z=father[y],d=direction(x),w=son[x][d^1];
    if(z)son[z][ms(z)==y?2:direction(y)]=x;
    son[x][d^1]=y;son[y][d]=w;
    if(w)father[w]=y;
    father[y]=x;father[x]=z;
    pushup(y,type);pushup(x,type);
    return;
}
void splay(int x,int type,int goal=0){
    pushall(x,ty);/*下传标记*/
    for(int y;y=father[x],(!isroot(x))&&y!=goal;rotate(x,ty)){
        if(father[y]!=goal&&(!isroot(y))){
            rotate(direction(x)^diretion(y)?x:y,type);
        }
    }
    return;
}

值得注意的是，direction 和 isroot 与普通 Splay 的不同。

因为无论你把这个点怎么转，这个点的中儿子是不会变的。

4.3 Access 类函数

access 函数意义是：将点 $x$ 旋转到整个 SATT 的根处，使点 $x$ 成为根簇的两个端点之一（另一端点即为 $T$ 的根节点），同时不能改变原树的结构和原树的根。

为了实现 access ，我们先将其旋转到其所在 compress tree 的树根，再把点$x$的右儿子“去掉”，使点 $x$ 成为其所在 compress tree 对应簇的端点。

if(rs(x)){
    int y=new_node();
    setfather(ms(x),y,0);
    setfather(rs(x),y,2);
    rs(x)=0;
    setfather(y,x,2);
    pushup(y,1);pushup(x,0);
}

如果这时点 $x$ 已经到了根部，则退出；若没有，则执行以下步骤，以让它跨过它上面的 rake tree ：

1. 将其父亲节点（一定是一个 rake node ）， splay 到其 rake tree 的树根；

2. 将 $x$ 的爷节点（一定是一个 compress node）splay 到其 compress tree 根部。

3. 若 $x$ 的爷节点有一个右儿子，则将点x和爷节点的右儿子互换，更新信息，然后退出。

4. 若爷节点没有右儿子，则先让点 $x$ 成为爷节点的右儿子，此时点 $x$ 原来的父节点没有中儿子，根据上文 rake node 的性质，它不能存在。于是调用 Delete 函数，将其删除，然后退出。

   1，2两个步骤合称为 local splay。3，4两个步骤合称为 splice。但我们方便起见，将它们都写在 splice 函数里。

上文提到的 Delete 函数是这样的：

1. 检视将要删除的点 $x$ 有没有左儿子，若有，则将左儿子的子树后继 splay 到点 $x$ 下方（成为新的左儿子），然后将右儿子（若有）变成左儿子的右儿子，此时点 $x$ 的左儿子就代替了点 $x$ 。（这相当于 splay 合并）

2. 若没有左儿子，则直接让其右儿子代替点$x$。

不难发现， splice 无非就是改变了原树的一些状态的端点选取，不影响最终状态的簇维护的信息。我们接下来一次 splice 完了之后的 点 $x$ 的父亲节点当作新的 点 $x$ ，进行下一次 splice。

最终我们会发现 我们最开始要操作的点 $x$ 一定在 根簇的 compress tree 最右端。我们只需最后做一次 global splay，将其旋至 SATT 根部即可。

// ls 一个SATT节点的左儿子
// rs 一个SATT节点的右儿子
// ms 一个SATT节点的中儿子
//son[x][0] ls
//son[x][1] rs
//son[x][2] ms
// type==1 在rake tree中
// type==0 在compress tree中
int new_node(){
    if(top){top--;return Stack[top+1];}
    else return ++tot; 
}
void setfather(int x,int fa,int type){
    if(x)father[x]=fa;son[fa][type]=x;
    return;
}
void Delete(int x){
    setfather(ms(x),father[x],1);
    if(ls(x)){
        int p=ls(x);pushdown(p,1);
        while(rs(p))p=rs(p),pushdown(p,1);
        splay(p,1,x);
        setfather(rs(x),p,1);
        setfather(p,father[x],2);
        pushup(p,1);pushup(father[x],0); 
    }
    else setfather(rs(x),father[x],2);Clear(x);
}
void splice(int x){
    /*  local splay */
    splay(x,1);int y=father[x];
    splay(y,0);pushdown(x,1);
    /*  splice  */
    if(rs(y)){
        swap(father[ms(x)],father[rs(y)]);
        swap(ms(x),rs(y));
    }
    else Delete(x);
    pushup(x,1);pushup(y,0);
    return;
}
void access(int x){
    splay(x,0);if(rs(x)){
        int y=new_node();
        setfather(ms(x),y,0);
        setfather(rs(x),y,2);
        rs(x)=0;
        setfather(y,x,2);
        pushup(y,1);pushup(x,0);
    }
    while(father[x]){
      splice(father[x]);x=father[x];pushup(x,0);
    }
    splay(x,0)/*global splay*/
    return;
}

关于 makeroot:

若要让一个点成为原树的根，那么我们就将点 $x$ access 到 SATT 的根节点，可知此时点 $x$ 已经是最终状态的簇一个端点。由 compress tree 的中序遍历性质可知，将点 $x$ 所在的 compress tree 左右颠倒（所有点的左右儿子互换），就使点 $x$ 成为原树的根。在具体实现中，我们通过给点 $x$ 打上一个翻转标记，不停下传来进行这一过程。

void makeroot(int x){
    access(x);
    push_rev(x);
    return;
}

于是就有 expose :

void expose(int x,int y){
    makeroot(x);
    access(y);
    return;
}

4.4 Link & Cut

现在我们要将原树中两个不连通的点之间连一条边，则我们先将其中的一个点 $x$ $makeroot$，再将另一个点 $y$ $access$ 到根，可知此时应该使点 $y$ 成为点 $x$ 的右儿子，并在点 $y$ 的右儿子上挂上这一条边（在只需维护点的 SATT 中，这一步可省）。

void Link(int x,int y,int z){
    /*z代表连接x,y的边*/
    access(x);makeroot(y);
    setfather(y,x,1);
    setfather(z,y,0);
    pushup(x,0);
    pushup(y,0);
    return;
}

Cut 跟 link 原理差不多……

void cut(int x,int y){
   expose(x,y);
   clear(rs(x));/*删掉xy这一基簇。*/
   father[x]=ls(y)=rs(x);
   pushup(y,0);
}

4.5 完整代码（Luogu P3690 【模板】动态树）

#include<bits/stdc++.h>
#define ls(x) T[x][0]
#define rs(x) T[x][1]
#define ms(x) T[x][2]
#define maxn 200005
using namespace std;
int read(){
    int s=0;
    char a=getchar();
    while(!isdigit(a))a=getchar();
    while(isdigit(a)){
        s=(s<<1)+(s<<3);
        s+=a^48;
        a=getchar();
    }
    return s;
}
int T[maxn][3],s[maxn][2],tot,v[maxn],n,m,r[maxn],top,st[maxn],f[maxn];
int nnd(){
    if(top){top--;return st[top+1];}
    else return ++tot; 
}
bool isr(int x){return rs(f[x])!=x&&ls(f[x])!=x;}
bool dir(int x){return rs(f[x])==x;} 
void psu(int x,int ty){
    if(ty){
        s[x][1]=s[ls(x)][1]^s[rs(x)][1]^s[ms(x)][1];return;
    }
    s[x][0]=s[ls(x)][0]^v[x]^s[rs(x)][0];
    s[x][1]=s[ls(x)][1]^s[ms(x)][1]^s[rs(x)][1]^v[x];
}
void psr(int x){if(!x)return;r[x]^=1;swap(ls(x),rs(x));}
void psd(int x,int ty){
    if(ty)return;
    if(r[x]){psr(ls(x));psr(rs(x));r[x]=0;return;}
}
void upd(int x,int ty){if(!isr(x))upd(f[x],ty);psd(x,ty); } 
void stf(int x,int fa,int ty){if(x)f[x]=fa;T[fa][ty]=x;return;}
void rtt(int x,int ty){
    int y=f[x],z=f[y],d=dir(x),w=T[x][d^1];
    if(z)T[z][ms(z)==y?2:dir(y)]=x;
    T[x][d^1]=y;T[y][d]=w;
    if(w)f[w]=y;f[y]=x;f[x]=z;
    psu(y,ty);psu(x,ty);
}
void spy(int x,int ty,int gl=0){
    upd(x,ty);for(int y;y=f[x],(!isr(x))&&y!=gl;rtt(x,ty)){
        if(f[y]!=gl&&(!isr(y)))rtt(dir(x)^dir(y)?x:y,ty);
    }
} 
void cle(int x){ls(x)=ms(x)=rs(x)=s[x][0]=s[x][1]=r[x]=v[x]=0;st[++top]=x; }
void del(int x){
    stf(ms(x),f[x],1);
    if(ls(x)){
        int p=ls(x);psd(p,1);while(rs(p))p=rs(p),psd(p,1);
        spy(p,1,x);stf(rs(x),p,1);stf(p,f[x],2);psu(p,1);psu(f[x],0); 
    }
    else stf(rs(x),f[x],2);cle(x);
}
void spl(int x){
    spy(x,1);int y=f[x];spy(y,0);psd(x,1);
    if(rs(y)){
        swap(f[ms(x)],f[rs(y)]);swap(ms(x),rs(y));psu(x,1);
    }
    else del(x);
    psu(rs(y),0);psu(y,0);
}
void acs(int x){
    spy(x,0);int ys=x;if(rs(x)){
        int y=nnd();stf(ms(x),y,0);stf(rs(x),y,2);
        rs(x)=0;stf(y,x,2);psu(y,1);psu(x,0);
    }
    while(f[x]){spl(f[x]);x=f[x];}spy(ys,0);
}
int fdr(int x){
    acs(x);psd(x,0);while(ls(x))x=ls(x),psd(x,0);spy(x,0);return x;
}
void mkr(int x){acs(x);psr(x);}
void epo(int x,int y){mkr(x);acs(y);}
void lnk(int x,int y){
    if(fdr(x)==fdr(y))return;
    acs(x);mkr(y);stf(y,x,1);
    psu(x,0);psu(y,0);
}
void cu(int x,int y){
    epo(x,y);if(ls(y)!=x||rs(x))return;
    f[x]=ls(y)=0;psu(y,0);
}
int main(){
    int i,j,op,U,V,n=read(),m=read();tot=n;
    for(i=1;i<=n;i++)v[i]=read(),psu(i,0);
    for(i=1;i<=m;i++){
        op=read();U=read();V=read();
        if(op==0){epo(U,V);cout<<s[V][0]<<'\n';}
        if(op==1)lnk(U,V);
        if(op==2)cu(U,V);
        if(op==3){acs(U);v[U]=V;psu(U,0);} 
    }
    return 0;
}

5.时间复杂度证明

5.1 势能分析

（如果你已经会势能分析了，你可以跳过 4.1 并直接看 4.2，或者自己证 SATT，%%%）

5.1-1 势能分析引入

在某个算法对于某一状态的某一操作中，定义这一次操作的均摊复杂度为：

$$a=c+{\phi }^{\prime }-\phi$$

其中 $c$ 是这一操作的实际复杂度，$\phi$ 是在操作之前状态的势能，而 ${\phi }^{\prime }$ 是这一操作后状态的势能。

势能是我们人为定义的，我们令 $\phi (x)$ 是状态 $x$ 的势能函数，势能函数的值仅与当前状态 $x$ 有关。上文中 $\phi ,{\phi }^{\prime }$ 是 $\phi (x),\phi (x^{\prime })$的缩写。

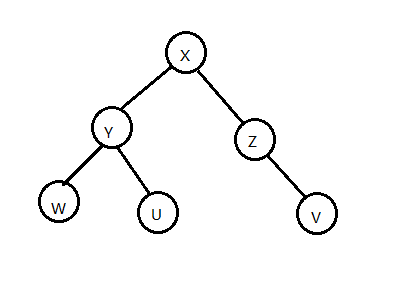
如图 4-1，为一棵有根树。

对于图中的有根树（点数 $n$ 等于 $6$），我们定义其势能函数 $\phi (x)=\sum _{i=1}^{n}r(i)$。

而 $r(x)=$ $\text{当前状态以 }x\text{ 为根的子树大小}$。

如图 4-2，为对上文有根树的进行一次操作后的状态。

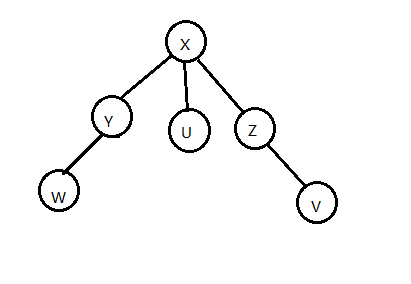
对于图 4-2 中的操作，我们知道这一操作的均摊复杂度为：

$$\begin{array}{rl}a& =c+{\phi }^{\prime }-\phi \\ & =1+\sum _{i=1}^n{r}^{\prime }(i)-\sum _{i=1}^{n}r(i)\\ & =1+r^{\prime }(Y)-r(Y)\\ & =1+2-1\\ & =2\end{array}$$

(假设这一操作实际复杂度是 $1$）

对于一系列操作的均摊复杂度，我们将每次操作均摊复杂度累加起来即可。下面设 $x_i$ 为第 $i$ 次操作后的状态，特别的，初始状态为 $x_0$ 。

$$\begin{array}{rl}\sum _{i=1}^m{a}_i& =\sum _{i=1}^m{c}_i+\sum _{i=1}^m(\phi (x_i)-\phi (x_{i-1}))\\ & =\sum _{i=1}^m{c}_i+\phi (x_n)-\phi (x_0)\end{array}$$ 则有 $$\sum c=\sum a-\phi (x_n)+\phi (x_0)$$

我们很多时候在某一个算法中，并不能直接求出 $\sum c$ 是多少，但我们可以构造势能函数 $\phi$ ，并通过一系列放缩手段，得到

$$\sum a\le \alpha$$

$$\phi (x_0)-\phi (x_n)\le \gamma$$

中的 $\alpha$ 和 $\gamma$ 大小。

那么就有

$$\sum c\le \alpha +\gamma$$

进而分析出实际时间复杂度了。

(以上只是势能函数应用的一部分，本文对势能函数的应用定义也并不严格)

5.1-2 Splay 复杂度证明

Splay 的时间复杂度要用 势能分析 来证明。

我们先来分析将某个点旋至根的 splay 的复杂度。

设在一棵 splay（点数为 $n$）中，其当前状态 $x$ 的势能函数为

$$\phi (x)=\sum _{i=1}^{n}r(i)$$

其中 $r(i)=\lceil {\log }_2(\text{以 }i\text{ 为根的子树大小})\rceil$。

一次 splay 函数可能有 zig/zag ，zig-zig/zag-zag，zig-zag/zag-zig 操作，我们下面对这三种操作分别分析。

zig / zag

如图 4-3，为 splay 的 zig/zag 操作。

我们只分析 zig 的均摊复杂度，因为 zag 只是将它左右颠倒了一下，分析过程相同，同理，下文中也只分析 zig-zig ，zig-zag 的复杂度。

值得注意的是，下面都假设 zig，zig-zig，zig-zag 的实际复杂度为$1$。

由图，zig均摊复杂度 $$\begin{array}{rl}a& =1+r^{\prime }(X)-r(X)+r^{\prime }(Y)-r(Y)\\ & \le 1+r^{\prime }(X)-r(X)\\ & \le 1+3(r^{\prime }(X)-r(X))\end{array}$$

我们就收缩到这一步，接下来分析 zig-zig 复杂度。

zig-zig / zag-zag

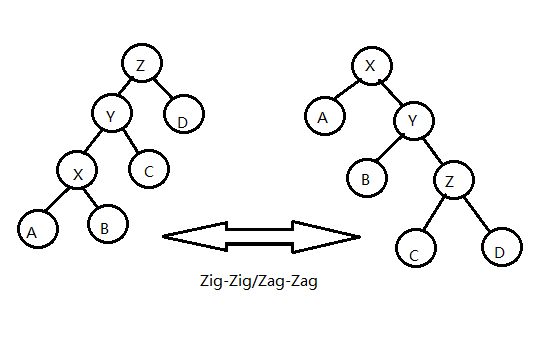
如图 4-4，为 splay 的 zig-zig\zag-zag 操作。

由图，zig-zig 的均摊复杂度

$$a=1+r^{\prime }(X)+r^{\prime }(Y)+r^{\prime }(Z)-r(X)-r(Y)-r(Z)$$

注意到 $2\lceil {\log }_2(a+b+c)\rceil -\lceil {\log }_2(a)\rceil -\lceil lo{g}_2(b)\rceil \ge 1(a,b,c\ge 1)$

所以有

$$1\le 2r^{\prime }(X)-r(X)-r(Z)$$

代回得

$$a\le 3r^{\prime }(X)-2r(X)+r^{\prime }(Z)+r^{\prime }(Y)-r(Y)-2r(Z)$$

注意到

$$r(Y)\ge r(X),r(Z)\ge r^{\prime }(Z),r(Z)\ge r^{\prime }(Y)$$

则有

$$0\le r(Y)-r(X)+r(Z)-r^{\prime }(Z)+r(Z)-r^{\prime }(Y)$$

相加得

$$a\le 3(r^{\prime }(X)-r(X))$$

这是一个理想的式子，化到这步为止。

zig-zag / zag-zig

如图 4-5，为 zig-zag 操作。

由图，zig-zag 操作的均摊复杂度

$$a=1+r^{\prime }(X)+r^{\prime }(Y)+r^{\prime }(Z)-r(X)-r(Y)-r(Z)$$

我们想把它化成和 zig-zig 中形式一致的式子，于是仿照 zig-zig 里的化法

$$1\le 2r^{\prime }(X)-r^{\prime }(Y)-r^{\prime }(Z)$$

代回得

$$a\le 3r^{\prime }(X)-r(X)-r(Y)-r(Z)$$

显然有

$$r(Y)\ge r(X),r(Z)\ge r(X)$$

$$0\le r(Y)-r(X)+r(Z)-r(X)$$

相加得

$$a\le 3(r^{\prime }(X)-r(X))$$

我们就达到了目的。

总复杂度分析

我们知道一个点是按以上这三种操作顺序执行才旋至根部的，而且旋转过程中，至多只会发生一次 zig\zag 操作；令 $r(X_i)$ 为第 $i$ 次操作执行后的状态中点 $X$ 的 $r$ 值，总共执行了 $m$ 次三种操作。于是一次 splay 的总均摊复杂度为

$$ \begin{aligned} a &\leq 3\sum_{i=1}^m (r(X_i)-r(X_{i-1})) +1\

&\leq 3(r(X_m)-r(X_0)) +1 \end{aligned} $$

而由 $r(x)$ 的定义，最终有

$$a\le 3\log n+1$$

我们现在来分析进行 $m$ 次 splay 操作的复杂度。

$$\sum _{i=1}^m{a}_i=\sum _{i=1}^m{c}_i+\phi (x_n)-\phi (x_0)$$

我们要求的是实际复杂度

$$\sum _{i=1}^m{c}_i=\sum _{i=1}^m{a}_i-\phi (x_n)+\phi (x_0)$$

由 $\phi (x)$ 的定义可知

$$\phi (x_0)-\phi (x_n)\le nlogn$$

又由上文我们对一次 splay 复杂度的证明，知

$$\sum _{i=1}^m{c}_i\le 3m\log n+m+n\log n$$

即证明了splay 复杂度的正确性。

对于 splay 以外的任何操作，我们都可以看作是常数复杂度或者给每次的旋转操作乘了个常数。对于后者，它使得每次 zig/zag 等操作实际复杂度不是 $1$。这似乎与我们在上文中的假设前提矛盾，但实际上这相当于给一次 splay 的复杂度乘了个常数；就以 zig-zig 操作为例，假如你现在每次 zig-zig 操作实际复杂度为 $2$。 $$ \begin{aligned} a &= 2 + r'(X) +r'(Y) +r'(Z) -r(X) -r(Y) -r(Z)\

&\leq 2(1 + r'(X) +r'(Y) +r'(Z) -r(X) -r(Y) -r(Z) )\ \end{aligned} $$ 发现只要做一样的分析即可。

5.2 SATT 时间复杂度证明

我们尝试将 splay 的成功经验搬到 SATT 上。

依然设在一棵 SATT（点数为$n$）中，其当前状态 $x$ 的势能函数为

$$\phi (x)=\sum _{i=1}^{n}r(i)$$

其中 $r(i)=\lceil {\log }_2(\text{以 }i\text{ 为根的子树大小})\rceil$。

则SATT的 splay 的均摊复杂度显然仍是 $3n\log n+1$，即使 SATT 是一个三叉树。

由splay 证完 splay 复杂度就能证得其它函数复杂度正确的经验可知，对于 SATT ,我们只要证得 access 函数复杂度正确，就能证得 SATT 的时间复杂度。

我们逐步分析 access 的均摊复杂度。

我们先要将点 $x$ 旋至 其所在 compress tree 的根，则这一步的均摊复杂度

$$a\le 3\log n+1$$

接着我们要使点 $x$ 无右儿子，则这一步的均摊复杂度

$$a=1+r^{\prime }(\gamma )-0\le \log n+1$$

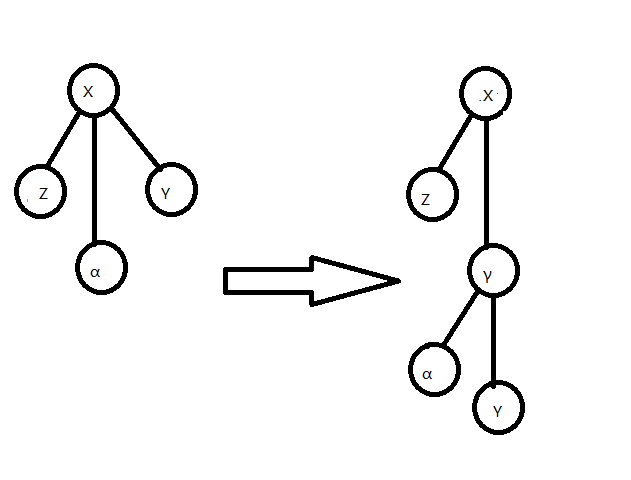
如图4-6 ，为去掉点 $x$ 的右儿子过程。

然后是 local splay ，splice 交替进行的过程，经过若干次 splice ，点 $x$ 被旋至 SATT 的根。我们对其中一组 local splay，splice 进行分析：

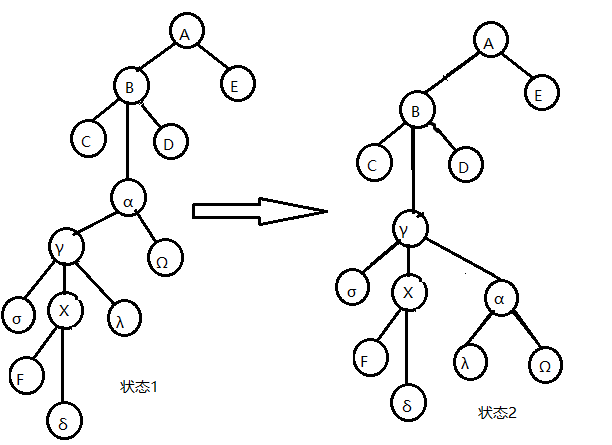
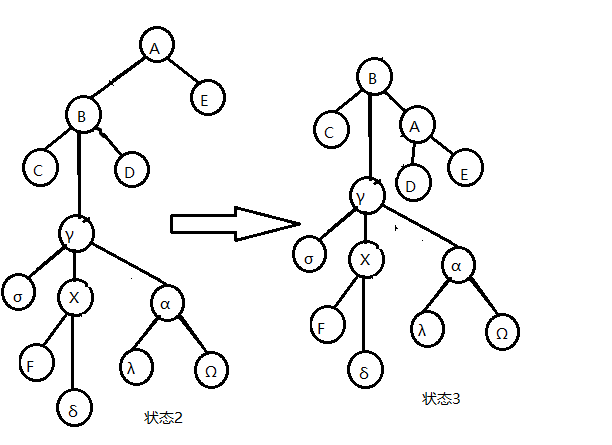
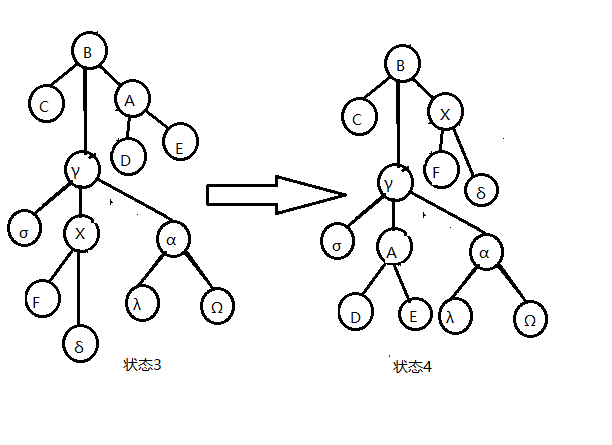
如图4-7，4-8，4-9,体现了对点 $x$ 做一次 splice的过程，不包括最后左旋点 $x$ 的部分。

为表达方便，设 $r_x(i)$为点 $i$ 在状态 $x$ 时的$r$值。

由图，易知由状态1到状态2的操作（将点 $x$ 的父亲旋至其 rake tree 的根部的 local splay 操作）的均摊复杂度

$$a\le 3(r_2(\gamma )-r_1(\gamma ))+1$$

由图，易知由状态 2 到状态 3 的操作（将点 $x$ 的爷节点旋至其 compress tree 的根部的 local splay 操作）的均摊复杂度

$$a\le 3(r_3(B)-r_2(B))+1$$

重点分析由状态3到状态4的操作（splice )

$$a=r_4(\gamma )-r_3(\gamma )+1$$

不难发现 $r_4(\gamma )\le r_3(B)$

故这一次操作的均摊复杂度为 $$\begin{array}{rl}a& \le r_3(B)-r_3(\gamma )+1\\ & \le 3(r_3(B)-r_3(\gamma ))+1\end{array}$$

综合上述过程，一次 splice 的复杂度为

$$a\le 3r_3(B)+3r_3(B)+3r_2(\gamma )-3r_3(\gamma )-3r_2(B)-3r_1(\gamma )+3$$

记下一次 splice 的点 $X$(即状态4中的点$B$)的$r$值为$r^{\prime }(X)$，并注意到

$$r_3(\gamma ),r_1(\gamma )\ge r_1(X)$$

$$r_3(B),r_2(\gamma )\le r^{\prime }(X)\text{ 且 }{r}_3(B)=r_2(B)$$

所以

$$a\le 9(r^{\prime }(X)-r(X))+3$$

除了上面这个复杂度以外，在 splice 中可能还会有因 delete 产生的额外均摊复杂度，记这一部分为 $a^{\prime }\le 3\log n+1$。

先不管 $a^{\prime }$ 部分，与 splay 复杂度证明中一样的事情，每次 splice 的 $r^{\prime }(X)$ 等于下一次的 $r(X)$ ，且第一次splice 的 $r(X)$ 等于我们一开始旋转点 $x$ 到其 compress tree 树根时的 $r(X)$ ，则对于不计 delete 的 一次 access 复杂度，我们有：

$$a\le 9(r^{\prime }(x)-r(x))+3k+1$$

其中 $k$ 为 splice 次数。

看样子 $a$ 会带一个 $3k+1$ 导致均摊复杂度无法分析，但我们有办法来对付它，注意到 zig-zig\zig-zag 的旋转可以这么均摊 $$\begin{array}{rl}a& \le 3(r^{\prime }(X)-r(X))+q\\ & \le 3(q-1)(r^{\prime }(X)-r(X))\end{array}$$

如果我们能“找到”足够多的 zig-zig，zig-zag 操作，我们就可以将这 $3k+1$ 平摊到 这些 操作上去，从而消掉 这个 $3k+1$。

我们发现 globel splay 里面就有这么多的 zig-zig，zag-zig 来给我们使用，因为 globel splay 里面点的个数一定大于 $k$，而从点 $x$ 到 globel splay 根部路径的点数一定不少于 $k$ ，也就是说一次 access 中一定会至少有 ${\displaystyle \frac{k}{2}}$ 个 zig-zag 操作，算上 globel access 的均摊复杂度 $a\le 3\log n+1$，一次 access 不记 delete 的均摊复杂度为 $$ \begin{aligned}

a &\leq 9(r'(X)-r(X)) + 3k + 1 + 18(r''(X)-r'(X)) -S+1 +3 \log n +1,S \ge 3k\

&a\leq 18(r''(X)-r(X)) +2 +3\log n+1\ &a\leq 21(r''(X)-r(X)) +3\

\end{aligned} $$

现在算上 $a^{\prime }$，像证明 splay 复杂度那样列出进行 $m$ 次 access 操作的总式子。

$$\sum _{i=1}^m{a}_i^{\prime }+\sum _{i=1}^m{a}_i=\sum _{i=1}^m{c}_i+\phi (x_n)-\phi (x_0)$$

我们要求的是实际复杂度

$$\sum _{i=1}^m{c}_i=\sum _{i=1}^m{a}_i+\sum _{i=1}^m{a}_i^{\prime }-\phi (x_n)+\phi (x_0)$$

$$\sum _{i=1}^m{c}_i\le \sum _{i=1}^m{a}_i^{\prime }+21m\log n+n\log n+3m$$

注意到 delete 操作的本质是删掉一个 rake node ，但我们在 $m$ 次操作中最多只会添加 $m$ 个 rake node，由 rake node 的定义，我们初始时最多有 $n$个 rake node，也就是说 我们总共只会做 $m+n$ 次 delete 操作，由 $a^{\prime }\le 3\log n+1$可知

$$\sum _{i=1}^m{c}_i\le 3(m+n)\log n+21m\log n+n\log n+4m+n$$

所以我们就证明了 access 的复杂度，而其他函数只不过是常数因子，所以我们就证明了 SATT 的复杂度。

顺便一提，如果你像写 LCT 一样省略 global splay 的过程，改为在每次 splice 时直接将要 access 的点旋转一下，这样做复杂度大概也是对的，我认为可以套用 《QTREE解法的一些研究 》这篇文章里面证明 LCT 时间复杂度的方法。（实测省略 global splay 的版本要快很多，能与LCT 在 Luogu P3690 跑得不分上下。。。）

6.例题

CF1192B Dynamic Diameter

维护动态直径，建出 SATT 后，我们只需要在 pushup 里面维护每个点的答案，最后查询根节点的答案（即整棵树的直径）就可以了。

void pushup(int x,int op){
    if(op==0){
                /*是compress node*/
        len[x]=len[ls(x)]+len[rs(x)];
        diam[x]=maxs[ls(x)][1]+maxs[rs(x)][0];
        diam[x]=max(diam[x],max(maxs[ls(x)][1],maxs[rs(x)][0])+maxs[ms(x)][0]);
        diam[x]=max(diam[x],max(max(diam[ls(x)],diam[rs(x)]),diam[ms(x)]));
        maxs[x][0]=max(maxs[ls(x)][0],len[ls(x)]+max(maxs[ms(x)][0],maxs[rs(x)][0]));
        maxs[x][1]=max(maxs[rs(x)][1],len[rs(x)]+max(maxs[ms(x)][0],maxs[ls(x)][1]));        
    }
    else{
                /*是rake node*/
        diam[x]=maxs[ls(x)][0]+maxs[rs(x)][0];
        diam[x]=max(diam[x],maxs[ms(x)][0]+max(maxs[ls(x)][0],maxs[rs(x)][0]));
        diam[x]=max(max(diam[x],diam[ms(x)]),max(diam[ls(x)],diam[rs(x)]));
        maxs[x][0]=max(maxs[ms(x)][0],max(maxs[ls(x)][0],maxs[rs(x)][0]));
    }
    return;
}

其中 diam 是当前点的答案（这个点代表的簇的直径）。len 表示当前 compress node 所在簇路径的长度，$max{s}_{0/1}$ 表示 compress node 到簇内点和端点的不选簇路径儿子/不选父亲的最大距离（如果是 rake node 则只存储选取当前簇的上端点到簇内点和端点的最大距离 $max{s}_0$）。每次查询 SATT 根节点的 diam 即可，正确性显然。

注意对 pushrev 做一些改动。

void pushrev(int x){
    if(!x)return;
    r[x]^=1;
    swap(ls(x),rs(x));
    swap(maxs[x][0],maxs[x][1]);
    return;
}

[CSP-S2019] 树的重心

假如我们能动态 $O(\log n)$ 维护树的重心，我们就做出这个题了。

SATT 支持动态 $O(\log n)$ 维护树的重心，做到这需要非局部搜索（non-local search）。

对于一种树上的性质，如果一个点/一条边在整棵树中有这种性质，且在所有包含它的子树中都包含此种性质，我们就称这个性质是局部的（local），否则称它是非局部的（non-local）。局部信息一般可以只通过 pushup 来维护

例如，权值最小值是局部的，因为一个点/一条边如果在整棵树中权值最小，那么在所有包含它的子树中它也是权值最小的，而权值第二小显然就是非局部的。

我们上文维护的 diam 也是局部信息。

回到正题，重心显然是一个非局部信息，无法通过简单的 pushup 来维护。我们考虑在 SATT 上搜索：

我们的搜索从 SATT 的根节点，即根簇开始。注意到重心有很好的性质：假如有一条边的一侧点的个数大于等于另一侧点的个数，那么边的这一侧一定至少有一个重心（重心可能有 $2$ 个）。

记 $sum$ 表示某一个簇的点个数，$maxs$ 为一棵 rake tree 的所有 rake node 中儿子的 $sum$ 最大值。

void pushup(int x,int op){
    if(op==0){        
        /*是 compress node*/
        sum[x]=sum[ls(x)]+sum[rs(x)]+sum[ms(x)]+1;
    }
    else{
        /*是 rake node*/
        maxs[x]=max(maxs[ls(x)],max(maxs[rs(x)],sum[ms(x)]));
        sum[x]=sum[ls(x)]+sum[rs(x)]+sum[ms(x)];
    }
    return;
}

现在我们在根簇

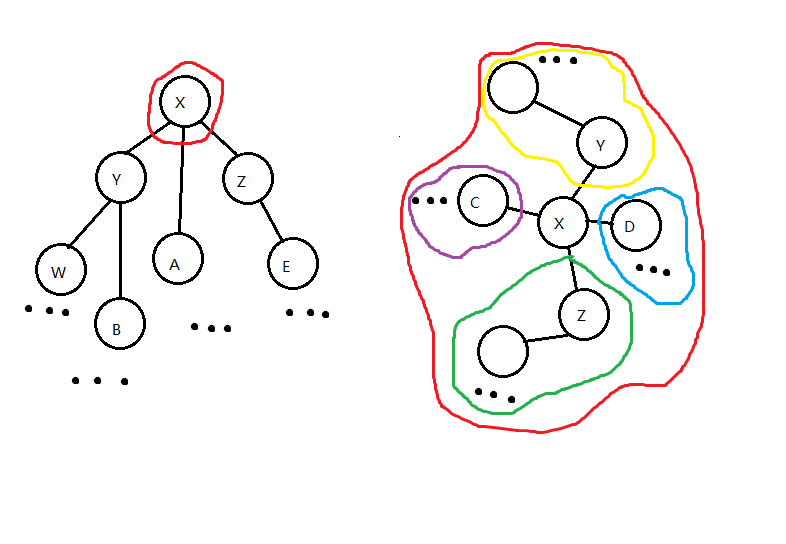
如图6-1，为在进行 non-local search 时的 SATT 和对应的 原树 $T$。

我们做如下比较：

1. 比较 簇 $compress(Y)$ 的 $sum$ 值与 簇 $compress(Z)$ 、簇 $A$ 和点 $X$ 的并(我们暂称为簇 $\alpha$ )的 $sum$ 值。若 $compress(Y)$ 的 $sum$ 值大于等于后者，说明至少有一个重心在 $compress(Y)$ 的子树中，我们递归到 $compress(Y)$ 搜索。（如果此处取等，点 $X$ 也是一个重心，需要记录）

2. 比较 簇 $compress(Z)$ 的 $sum$ 值与 簇 $compress(Y)$ 、簇 $A$ 和点 $X$ 的并(我们暂称为簇 $\beta$ )的 $sum$ 值。若 $compress(Z)$ 的 $sum$ 值大于等于后者，说明至少有一个重心在 $compress(Z)$ 的子树中，我们递归到 $compress(Z)$ 搜索。（如果此处取等，点 $X$ 也是一个重心，需要记录）

3. 比较 点 $x$ 中儿子 rake tree 之中 $sum$ 最大的更小簇（见3-2）的 $sum$ 值与 簇 $compress(Y)$ 、簇 $A$ 、点 $X$ 及其它更小簇的并(我们暂称为簇 $\gamma$ )的 $sum$ 值，若 那个更小簇 的 $sum$ 值大于等于后者，说明至少有一个重心在 那个更小簇的 子树中，我们递归到它搜索。（如果此处取等，点 $X$ 也是一个重心，需要记录）

4. 若以上比较都不递归，则点 $X$ 一定是一个重心，记录并退出。

第一步的搜索显然正确，之后应该怎么搜呢？

假如我们递归到 $Y$ ，则现在 $Y$ 储存信息的并不完整，因为 $compress(Y)$ 里面只存储了它自己这个簇的信息，而我们要求的是整棵树的重心。解决方法是，将之前簇的信息记录下来，在点 $Y$ 上比较计算时将上一个簇的信息与 点 $Y$ 自己的信息合并处理。具体实现如下：

void non_local_search(int x,int lv,int rv,int op){

   /*lv 和 rv 都是搜索的上一个簇的信息*/

    if(!x)return;psd(x,0);
    if(op==0){
        if(maxs[ms(x)]>=sum[ms(x)]-maxs[ms(x)]+sum[rs(x)]+sum[ls(x)]+lv+1+rv){
            if(maxs[ms(x)]==sum[ms(x)]-maxs[ms(x)]+sum[rs(x)]+sum[ls(x)]+lv+1+rv){
                if(ans1)ans2=x;else ans1=x;
            }
            non_local_search(ms(x),sum[ms(x)]-maxs[ms(x)]+sum[rs(x)]+sum[ls(x)]+1+lv+rv,0,1);return;                
        }
        if(ss[rs(x)]+rv>=ss[ms(x)]+ss[ls(x)]+lv+1){
            if(ss[rs(x)]+rv==ss[ms(x)]+ss[ls(x)]+lv+1){
                if(ans1)ans2=x;else ans1=x;
            }
            non_local_search(rs(x),sum[ms(x)]+1+sum[ls(x)]+lv,rv,0);return;
        }    
        if(sum[ls(x)]+lv>=sum[ms(x)]+sum[rs(x)]+1+rv){
            if(sum[ls(x)]+lv==sum[ms(x)]+sum[rs(x)]+1+rv){
                if(ans1)ans2=x;else ans1=x;
            }
            non_local_search(ls(x),lv,rv+sum[ms(x)]+1+sum[rs(x)],0);return;
        }            
    }
    else{
        if(maxs[ls(x)]==maxs[x]){non_local_search(ls(x),lv,rv,1);return;}
        if(maxs[rs(x)]==maxs[x]){non_local_search(rs(x),lv,rv,1);return;}
        non_local_search(ms(x),lv,rv,0);
        return;
    }
    if(ans1)ans2=x;else ans1=x;return;
}

完整代码如下：

#include<bits/stdc++.h>
#define ls(x) T[x][0]
#define rs(x) T[x][1]
#define ms(x) T[x][2]
#define maxn 1000005
using namespace std;
int read(){
    int s=0;
    char a=getchar();
    while(!isdigit(a))a=getchar();
    while(isdigit(a)){
        s=(s<<1)+(s<<3);
        s+=a^48;
        a=getchar();
    }
    return s;
}
int T[maxn][3],tot,n,m,r[maxn],top,st[maxn],f[maxn],maxs[maxn],ss[maxn];
int nnd(){
    if(top){top--;return st[top+1];}
    else return ++tot; 
}
bool isr(int x){return rs(f[x])!=x&&ls(f[x])!=x;}
bool dir(int x){return rs(f[x])==x;} 
void psr(int x){if(!x)return;r[x]^=1;swap(ls(x),rs(x));}
void psd(int x,int ty){
    if(ty)return;
    if(r[x]){psr(ls(x));psr(rs(x));r[x]=0;return;}
}
void psu(int x,int op){
    psd(x,op);/*不知道哪没 psd*/
    if(op==0){        
        ss[x]=ss[ls(x)]+ss[rs(x)]+ss[ms(x)]+1;
    }
    else{
        maxs[x]=max(maxs[ls(x)],max(maxs[rs(x)],ss[ms(x)]));
        ss[x]=ss[ls(x)]+ss[rs(x)]+ss[ms(x)];
    }
    return;
}
void upd(int x,int ty){if(!isr(x))upd(f[x],ty);psd(x,ty); } 
void stf(int x,int fa,int ty){if(x)f[x]=fa;T[fa][ty]=x;return;}
void rtt(int x,int ty){
    int y=f[x],z=f[y],d=dir(x),w=T[x][d^1];
    if(z)T[z][ms(z)==y?2:dir(y)]=x;
    T[x][d^1]=y;T[y][d]=w;
    if(w)f[w]=y;f[y]=x;f[x]=z;
    psu(y,ty);psu(x,ty);
}
void spy(int x,int ty,int gl=0){
    upd(x,ty);for(int y;y=f[x],(!isr(x))&&y!=gl;rtt(x,ty)){
        if(f[y]!=gl&&(!isr(y)))rtt(dir(x)^dir(y)?x:y,ty);
    }
} 
void cle(int x){ls(x)=ms(x)=rs(x)=ss[x]=r[x]=maxs[x]=f[x]=0;st[++top]=x; }
void del(int x){
    stf(ms(x),f[x],1);
    if(ls(x)){
        int p=ls(x);psd(p,1);while(rs(p))p=rs(p),psd(p,1);
        spy(p,1,x);stf(rs(x),p,1);stf(p,f[x],2);psu(p,1);psu(f[x],0); 
    }
    else stf(rs(x),f[x],2);cle(x);
}
void spl(int x){
    spy(x,1);int y=f[x];spy(y,0);psd(x,1);
    if(rs(y)){
        swap(f[ms(x)],f[rs(y)]);swap(ms(x),rs(y));
    }
    else del(x);psu(x,1);psu(y,0);rtt(rs(y),0);
}
void acs(int x){
    spy(x,0);if(rs(x)){
        int y=nnd();stf(ms(x),y,0);stf(rs(x),y,2);
        rs(x)=0;stf(y,x,2);psu(y,1);psu(x,0);
    }
    while(f[x])spl(f[x]);
}
void mkr(int x){acs(x);psr(x);}
void epo(int x,int y){mkr(x);acs(y);}
void lnk(int x,int y){acs(x);mkr(y);stf(y,x,1);psu(x,0);}
void cu(int x,int y){epo(x,y);f[x]=ls(y)=0;psu(y,0);}
int ans1,ans2;
void non_local_search(int x,int lv,int rv,int op){
    if(!x)return;psd(x,0);
    if(op==0){
        if(maxs[ms(x)]>=ss[ms(x)]-maxs[ms(x)]+ss[rs(x)]+ss[ls(x)]+lv+1+rv){
            if(maxs[ms(x)]==ss[ms(x)]-maxs[ms(x)]+ss[rs(x)]+ss[ls(x)]+lv+1+rv){
                if(ans1)ans2=x;else ans1=x;
            }
            non_local_search(ms(x),ss[ms(x)]-maxs[ms(x)]+ss[rs(x)]+ss[ls(x)]+1+lv+rv,0,1);return;                
        }
        if(ss[rs(x)]+rv>=ss[ms(x)]+ss[ls(x)]+lv+1){
            if(ss[rs(x)]+rv==ss[ms(x)]+ss[ls(x)]+lv+1){
                if(ans1)ans2=x;else ans1=x;
            }
            non_local_search(rs(x),ss[ms(x)]+1+ss[ls(x)]+lv,rv,0);return;
        }    
        if(ss[ls(x)]+lv>=ss[ms(x)]+ss[rs(x)]+1+rv){
            if(ss[ls(x)]+lv==ss[ms(x)]+ss[rs(x)]+1+rv){
                if(ans1)ans2=x;else ans1=x;
            }
            non_local_search(ls(x),lv,rv+ss[ms(x)]+1+ss[rs(x)],0);return;
        }            
    }
    else{
        if(maxs[ls(x)]==maxs[x]){non_local_search(ls(x),lv,rv,1);return;}
        if(maxs[rs(x)]==maxs[x]){non_local_search(rs(x),lv,rv,1);return;}
        non_local_search(ms(x),lv,rv,0);
        return;
    }
    if(ans1)ans2=x;else ans1=x;return;
}
int qu[maxn],qv[maxn];
int main(){
    int i,TT=read(),n,I,U,V,x;long long ANS;
    for(I=1;I<=TT;I++){
        n=read();tot=n;ANS=0;
        for(i=1;i<=n;i++)ss[i]=1;
        for(i=1;i<=n-1;i++){
            qu[i]=U=read();qv[i]=V=read();lnk(U,V);
        }
        for(i=1;i<=n-1;i++){
            cu(qu[i],qv[i]);
            ans1=0;ans2=0;non_local_search(qu[i],0,0,0);
            ANS+=ans1+ans2;
            if(ans1)acs(ans1);if(ans2)acs(ans2);
            ans1=0;ans2=0;non_local_search(qv[i],0,0,0);
            ANS+=ans1+ans2;
            if(ans1)acs(ans1);if(ans2)acs(ans2);    
            lnk(qu[i],qv[i]);    
        }
        cout<<ANS<<'\n';
        for(i=1;i<=tot;i++)T[i][0]=T[i][1]=T[i][2]=ss[i]=r[i]=maxs[i]=f[i]=0;
        tot=top=0;
    }
    return 0;
}

7.参考资料

1.《Self-Adjusting Top Trees Robert》E. Tarjan， Renato F. Werneck。

2.negiizhao的博客（%%论文哥）

3.zhengrunzhe的sone1题解（%%zhengrunzhe）